Skip to contents

G-computation Algorithms in tvmedg

Source: vignettes/tvmedg_algorithms.Rmd
tvmedg_algorithms.Rmd

Background

Notations

  • Let AA denote the exposure of interest, taking values aa and a*a^\ast. Let YY be the outcome, MM the mediator, LL the time-varying confounder, and vv the vector of pre-exposure (time-fixed) covariates.

  • Let YaY_a and MaM_a denote the values of the outcome and mediator, respectively, that would have been observed had the exposure AA been set to aa; similarly, Ya*Y_{a^\ast} and Ma*M_{a^\ast} represent the potential values under A=a*A = a^\ast.

The average total effect can be then decomposed into natural direct and indirect effects as:

E(Ya−Ya*)=E(YaMa−Ya*Ma*)=E(YaMa−YaMa*)⏟Natural indirect effect+E(YaMa*−Ya*Ma*)⏟Natural direct effect E(Y_a - Y_{a^*}) = E(Y_{aM_{a}} - Y_{a^*M_{a^*}}) = \underbrace{E(Y_{aM_{a}} - Y_{aM_{a^*}})}_{\text{Natural indirect effect}} + \underbrace{E(Y_{aM_{a^*}} - Y_{a^*M_{a^*}})}_{\text{Natural direct effect}}

The potential outcomes YaMaY_{aM_a} and Ya*Ma*Y_{a^\ast M_{a^\ast}} represent the values of the outcome under exposure levels aa and a*a^\ast, respectively, with the mediator taking its natural value under each exposure. In contrast, YaMa*Y_{aM_{a^\ast}} describes the outcome under exposure aa, but with the mediator set to the value it would have taken under a*a^\ast, capturing a cross-world scenario relevant to mediation analysis.

In the context of mediator–outcome confounders being affected by the exposure (i.e., $Y_{am} \not\!\perp\!\!\!\perp M_{a^*}|V$ - violation of identification condition), the natural direct and indirect effect above are not identified. The randomized interventional analogues were introduced.

Let Ga|vG_{a|v} denote the a random draw from the distribution of the mediator with exposure AA is set at aa conditional on covariates vv. In other words, GG reflects a stochastic draw from its conditional distribution rather than a fixed potential value of the mediator. The randomized interventional analogues of natural direct and indirect effects are defined as

E(YaGa∣v)−E(Ya*Ga*∣v)=E(YaGa∣v)−E(YaGa*∣v)+E(YaGa*∣v)−E(Ya*Ga*∣v) E(Y_{aG_{a} \mid v}) - E(Y_{a^*G_{a^*} \mid v}) = E(Y_{aG_{a} \mid v}) - E(Y_{aG_{a^*} \mid v}) + E(Y_{aG_{a^*} \mid v}) - E(Y_{a^*G_{a^*} \mid v})

In the longitudinal setting, the overbars denote the history of variables up to time tt. The total effect of a longitudinal exposure regime a‾\bar{a} versus a‾*\bar{a}^* can be decomposed as:

E(Ya‾G‾a‾∣v∣v)−E(Ya‾*G‾a‾*∣v∣v)=E(Ya‾G‾a‾∣v∣v)−E(Ya‾G‾a‾*∣v∣v)⏟interventional indirect effect+E(Ya‾G‾a‾*∣v∣v)−E(Ya‾*G‾a‾*∣v∣v)⏟interventional direct effect. E(Y_{\bar{a} \bar{G}_{\bar{a} \mid v}} \mid v) - E(Y_{\bar{a}^* \bar{G}_{\bar{a}^* \mid v}} \mid v) = \underbrace{E(Y_{\bar{a} \bar{G}_{\bar{a} \mid v}} \mid v) - E(Y_{\bar{a} \bar{G}_{\bar{a}^* \mid v}} \mid v)}_{\text{interventional indirect effect}} + \underbrace{E(Y_{\bar{a} \bar{G}_{\bar{a}^* \mid v}} \mid v) - E(Y_{\bar{a}^* \bar{G}_{\bar{a}^* \mid v}} \mid v)}_{\text{interventional direct effect}}.

As shown by VanderWeele and Tchetgen Tchetgen (2017), the interventional analogues of natural direct and indirect effects, under the causal DAG (below) where the mediator precedes the time-varying confounder (MM preceding LL), can be identified using the so-called mediational g-formula.

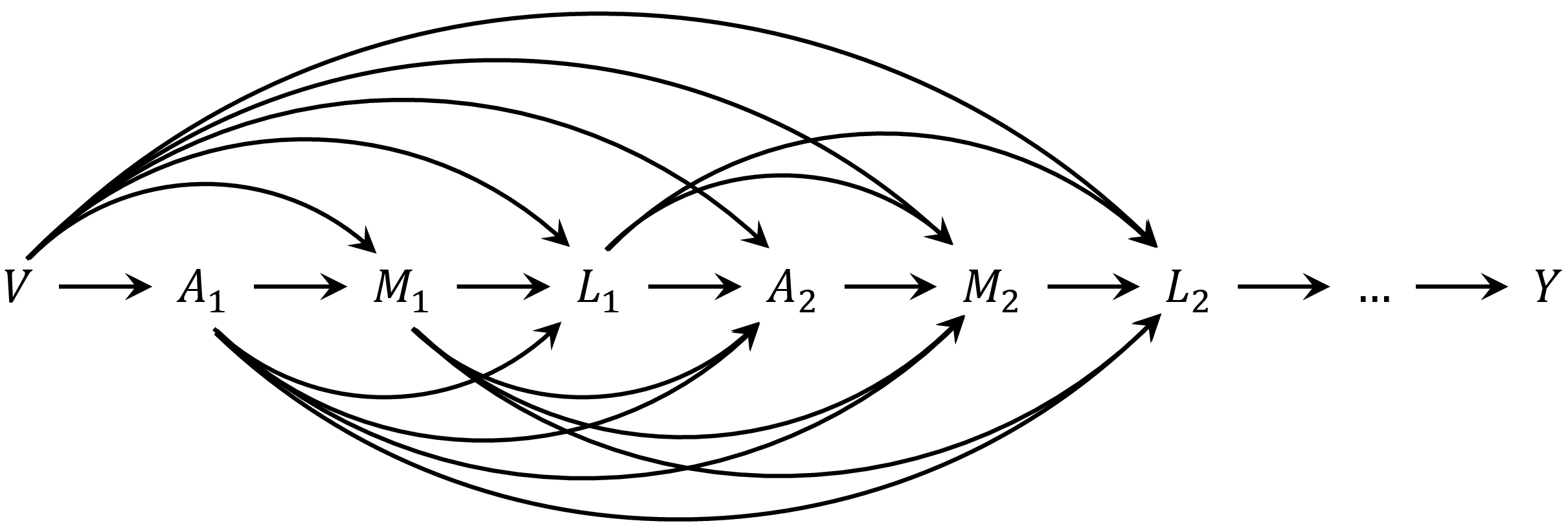
DAG for the context that the mediator precedes the time-varying confounder

DAG for the context that the mediator precedes the time-varying confounder

In particular, the identification of E(Ya‾G‾a‾*∣v∣v)E(Y_{\bar{a} \bar{G}_{\bar{a}^*}\mid v} \mid v) is

E(Ya‾G‾a‾*∣v∣v)=∫m‾∫l‾(T−1)E(Y∣a‾,m‾,l‾,v)∏t=1T−1dP(l‾(t)∣a‾(t),m‾(t),l‾(t−1),v)×[∫l‾†(T−1)∏t=1TP(m(t)∣a‾*(t),m‾(t−1),l‾†(t−1),v)dP(l‾†(t−1)∣a‾*(t−1),m‾(t−1),l‾†(t−2),v)]\begin{align*} E(Y_{\bar{a} \bar{G}_{\bar{a}^*}\mid v} \mid v) = &\int_{\bar{m}} \int_{\bar{l}(T-1)} E(Y \mid \bar{a}, \bar{m}, \bar{l}, v) \prod_{t=1}^{T-1} dP\left( \bar{l}(t) \mid \bar{a}(t), \bar{m}(t), \bar{l}(t-1), v \right) \\ &\times \left[ \int_{\bar{l}^\dagger(T-1)} \prod_{t=1}^{T} P\left( m(t) \mid \bar{a}^*(t), \bar{m}(t-1), \bar{l}^\dagger(t-1), v \right) \, dP\left( \bar{l}^\dagger(t-1) \mid \bar{a}^*(t-1), \bar{m}(t-1), \bar{l}^\dagger(t-2), v \right) \right] \end{align*}

In the context where time-varying confounder precedes the mediator (LL preceding MM)

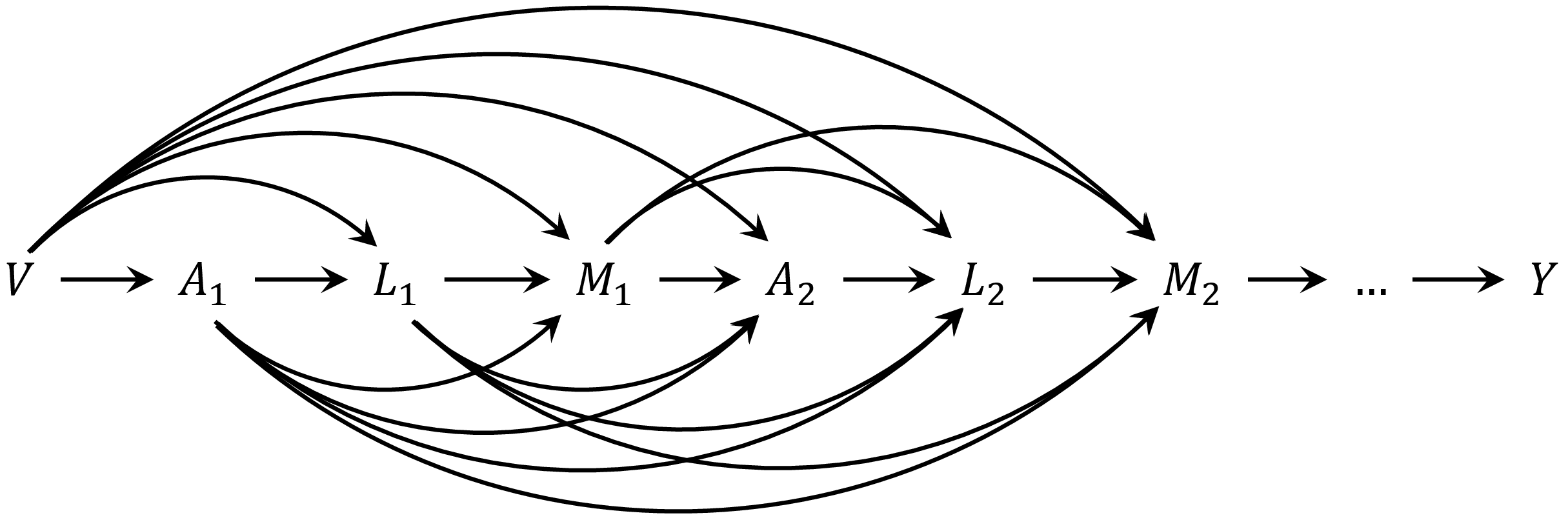
DAG for the context that the time-varying confounder precedes the mediator

DAG for the context that the time-varying confounder precedes the mediator

The mediational g-formula identification for E(Ya‾G‾a‾*∣v∣v)E(Y_{\bar{a} \bar{G}_{\bar{a}^*}\mid v} \mid v) becomes

E(Ya‾G‾a‾*∣v∣v)=∫m‾∫l‾(T−1)E(Y∣a‾,m‾,l‾,v)∏t=1T−1dP(l‾(t)∣a‾(t),m‾(t−1),l‾(t−1),v)×d[∫l‾†(T−1)∏t=1TP(m(t)∣a‾*(t),m‾(t−1),l‾†(t),v)dP(l‾†(t)∣a‾*(t),m‾(t−1),l‾†(t−1),v)].\begin{align*} E(Y_{\bar{a} \bar{G}_{\bar{a}^*}\mid v} \mid v) = &\int_{\bar{m}} \int_{\bar{l}(T-1)} E(Y \mid \bar{a}, \bar{m}, \bar{l}, v) \prod_{t=1}^{T-1} dP\left( \bar{l}(t) \mid \bar{a}(t), \bar{m}(t-1), \bar{l}(t-1), v \right) \\ &\times d\left[ \int_{\bar{l}^\dagger(T-1)} \prod_{t=1}^{T} P\left( m(t) \mid \bar{a}^*(t), \bar{m}(t-1), \bar{l}^\dagger(t), v \right) \, dP\left( \bar{l}^\dagger(t) \mid \bar{a}^*(t), \bar{m}(t-1), \bar{l}^\dagger(t-1), v \right) \right]. \end{align*}

For ease of notation, let’s adopt the same shorthand notations as in the VanderWeele and Tchetgen Tchetgen (2017) paper: Q(a,a)Q(a, a) to represent E(Ya‾G‾a‾∣v∣v)E(Y_{\bar{a} \bar{G}_{\bar{a}}\mid v} \mid v), Q(a,a*)Q(a, a^*) for E(Ya‾G‾a‾*∣v∣v)E(Y_{\bar{a} \bar{G}_{\bar{a}^*}\mid v} \mid v), and Q(a*,a*)Q(a^*, a^*) for E(Ya‾*G‾a‾*∣v∣v)E(Y_{\bar{a}^* \bar{G}_{\bar{a}^*}\mid v} \mid v),

G-computation Algorithms in tvmedg

tvmedg implements g-computation to estimate interventional direct and indirect effects in longitudinal settings, based on the mediational g-formula mentioned above. The core algorithm involves 4 main steps:

  • Step 1: Fitting parametric models

    tvmedg() fits the user-specified regression models for each time-varying variable, conditional on relevant history and baseline covariates:

    • Time-varying confounders:
      • E(L‾(t)∣a‾(t),m‾(t),l‾(t−1),v)E(\bar{L}(t) \mid \bar{a}(t), \bar{m}(t), \bar{l}(t-1), v) if (MM preceding LL)
      • E(L‾(t)∣a‾(t),m‾(t−1),l‾(t−1),v)E(\bar{L}(t) \mid \bar{a}(t), \bar{m}(t-1), \bar{l}(t-1), v) if (LL preceding MM)
    • Mediator:
      • E(M(t)∣a‾*(t),m‾(t−1),l‾†(t−1),v)E(M(t) \mid \bar{a}^*(t), \bar{m}(t-1), \bar{l}^\dagger(t-1), v)
    • Outcome:
      • E(Y∣a‾,m‾,l‾,v)E(Y \mid \bar{a}, \bar{m}, \bar{l}, v)

  • Step 2: Monte Carlo sampling
    Resample the values of all variables at baseline, including time-fixed covariates VV and time-varying confounders LL at time t=0t = 0. This step approximates the baseline covariate distribution and improves the stability and precision of predictions in Step 3.

  • Step 3: Predict follow-up
    Using the baseline samples generated in Step 2, Step 3 simulates follow-up trajectories by sequentially predicting time-varying confounders, mediators, and outcomes under specified exposure regimes. This process is illustrated in the following figure (as an example for estimating Q(a,a*)Q(a, a^*)) in the context of binary outcome.

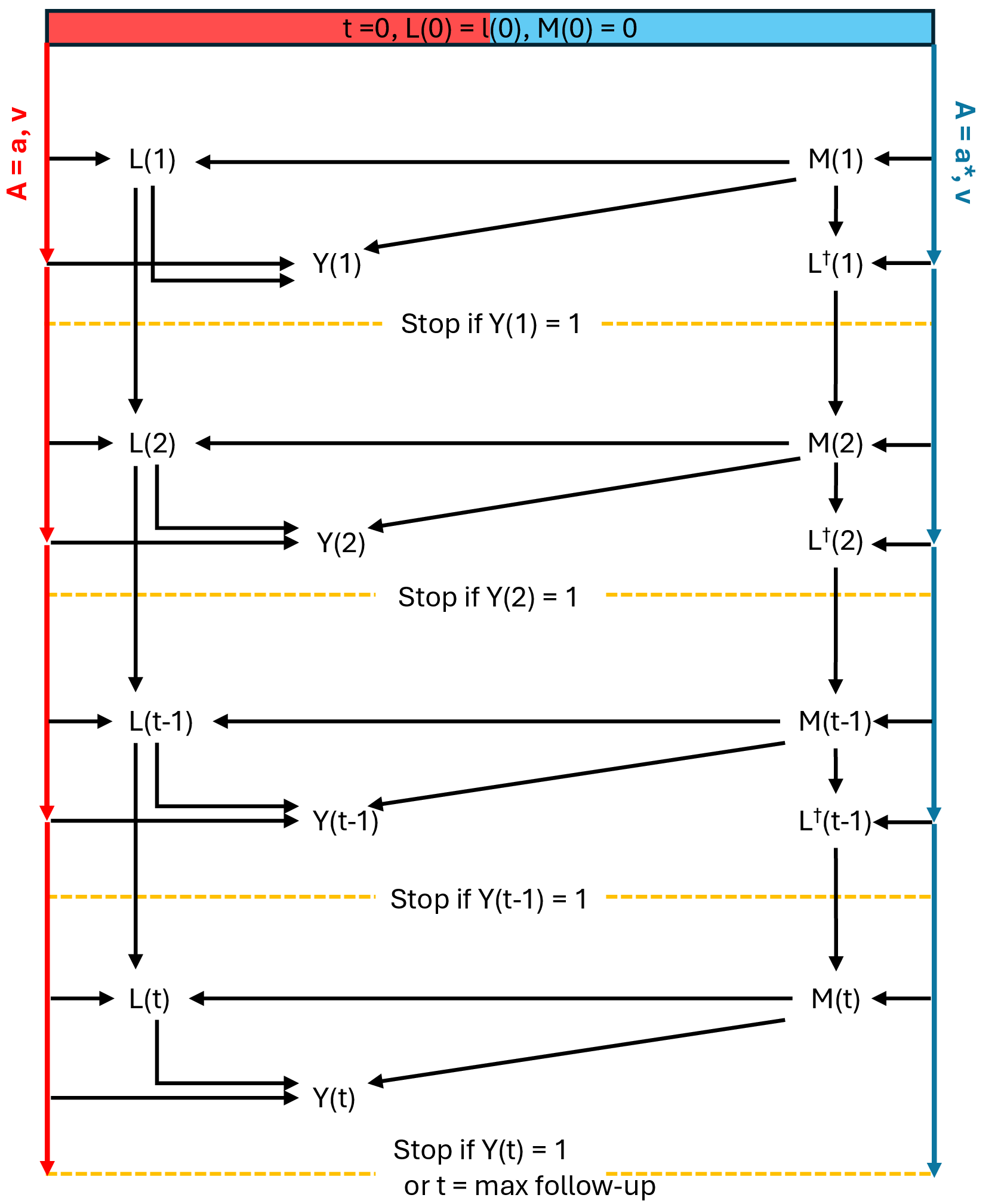
g-computation in tvmedg

g-computation in tvmedg

  • Step 4: Estimating interventional analogues of natural direct and indirect effects
    Estimating Q(a,a)Q(a, a), Q(a,a*)Q(a, a^*), and Q(a*,a*)Q(a^*, a^*) at the end of follow-up and derive:

    • Interventional total effect (rTE): Q(a,a)−Q(a*,a*)Q(a, a) - Q(a^*, a^*)

    • Interventional direct effect (rDE): Q(a,a*)−Q(a*,a*)Q(a, a^*) - Q(a^*, a^*)

    • Interventional indirect effect: Q(a,a)−Q(a,a*)Q(a, a) - Q(a, a^*)

    • Proportional explain: Indirect effect / Total effect

References

VanderWeele, T. (2015). Explanation in causal inference: methods for mediation and interaction. Oxford University Press.

VanderWeele, T. J., & Tchetgen Tchetgen, E. J. (2017). Mediation analysis with time varying exposures and mediators. Journal of the Royal Statistical Society Series B: Statistical Methodology, 79(3), 917-938.